
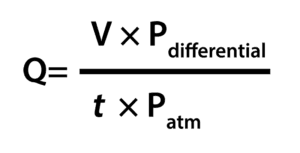
This is a useful property of all proportionalities: simply insert values (expressed in any unit of measurement) determined by physical experiment and solve for the proportionality constant’s value to satisfy the expression as an equation In other words, we may use the constant of proportionality (k) as a unit-of-measurement correction factor as well as a definition of element geometry. However, if we happen to know the differential pressure produced by any particular flow element tube with any particular fluid density at a specified flow rate (real-life conditions), we may calculate a value for k in the short equation that makes all those measurements “agree” with one another. If we wish to use more convenient units of measurement such as inches of water column for pressure and specific gravity (unitless) for density, the original (longer) equation simply will not work. We cannot arbitrarily choose different units of measurement for these variables, because the units must “agree” with one another. If we define k by the mouth and throat areas (A1, A2) of any particular venturi tube, we must be very careful to express the pressures and densities in compatible units of measurement.įor example, with k strictly defined by flow element geometry (tube areas measured in square feet), the calculated flow rate (Q) must be in units of cubic feet per second, the pressure values P1 and P2 must be in units of pounds per square foot, and mass density must be in units of slugs per cubic foot. This equation is a simplified version of the one derived from the physical construction of a venturi tube:Īs you can see, the constant of proportionality (k) shown in the simpler equation is nothing more than a condensation of the first half of the longer equation: k represents the geometry of the venturi tube. Contact Omega engineering for details.As we saw in the previous article, we may derive a relatively simple equation for predicting flow through a fluid-accelerating element given the pressure drop generated by that element and the density of the fluid flowing through it: Volumetric Flow Calculations Wetted Parts: 303 & 302 Stainless Steel, FKM Heat Cured Silicone Rubber, Glass Reinforced Polyphenylene Sulfide, Heat Cured Epoxy, Aluminum, Gold, Silicon, Glass. Supply Current: 35 mA typical current draw 100 mA available supply recommended Supply Voltage: 7 to 30 Vdc (15 to 30 Vdc for 4 to 20 mA output) The primary trade-off for response time is signal noise A variable register allows response time to be field adjustable to a certain extent via RS232 communications. Response Time: 10 ms typical default response time for 63.2% of a step change.
#Volumetric flow portable
These flowmeters are also available in a portable version for use in the field (-B models).
#Volumetric flow serial
It is also possible to multi-drop up to 26 units on the same serial connection to a distance of 125'. Volumetric flow, mass flow, or absolute pressure, and temperature can be viewed or recorded through the RS232 connection. The gas select feature can be adjusted from the front of the keypad or via RS232 communications.

Standard units include a 0 to 5 V output (4 to 20 mA optional) and RS232 communications. This standardized flow rate is commonly called the mass flow rate and is reported in units such as standard cubic feet per minute (SCFM) or standard liters per minute (SLM). Separate absolute temperature and pressure sensors are incorporated and correct the volumetric flow rate to a set of standard conditions. This, along with the viscosity of the gas, is used to accurately determine the volumetri flow rate. Inside this region, the Poiseuille equation dictates that the volumetric flow rate be linearly related to the pressure drop along a fixed distance of the LFE. A laminar flow element (LFD) insdie the meter forces the gas into laminar (streamlined) flow.
#Volumetric flow series
The FMA-1600A Series mass and volumetric Omega's flow meters use the principle of differential pressure within a laminar flow field to determine the mass flow rate.


 0 kommentar(er)
0 kommentar(er)
